Project 4: ClothSim

Overview

In this project, we simulated cloth behavior using a mass-spring system.

Essentially, a cloth can be approximated as a uniform grid of point masses all connected using ideal springs. There are three types of springs that give cloths their physical behavior:

• Structural springs connect point masses with immediately adjacent point masses (top, bottom, left, right).
• Shearing springs connect point masses with diagonal point masses (top left, top right, bottom left, bottom right).
• Bending springs connect point masses with adjacent point masses separated by one (2 from top, 2 from bottom, 2 from left, 2 from right). These springs are weaker than the other two spring constraints.

After constructing the cloth using point masses and spring constraints, we can then apply external forces, such as gravity or normal forces due to collisions, to affect how the cloth moves. In this project, we handle collisions with spheres, planes, and with the cloth itself (such that it doesn’t overlap itself).

Finally, we implemented shaders, textures, bump maps, and reflections to improve the appearance of the cloth.

Part 1: Masses and Springs

In this part, we constructed the basic cloth grid of point masses and spring constraints as described in the introduction.

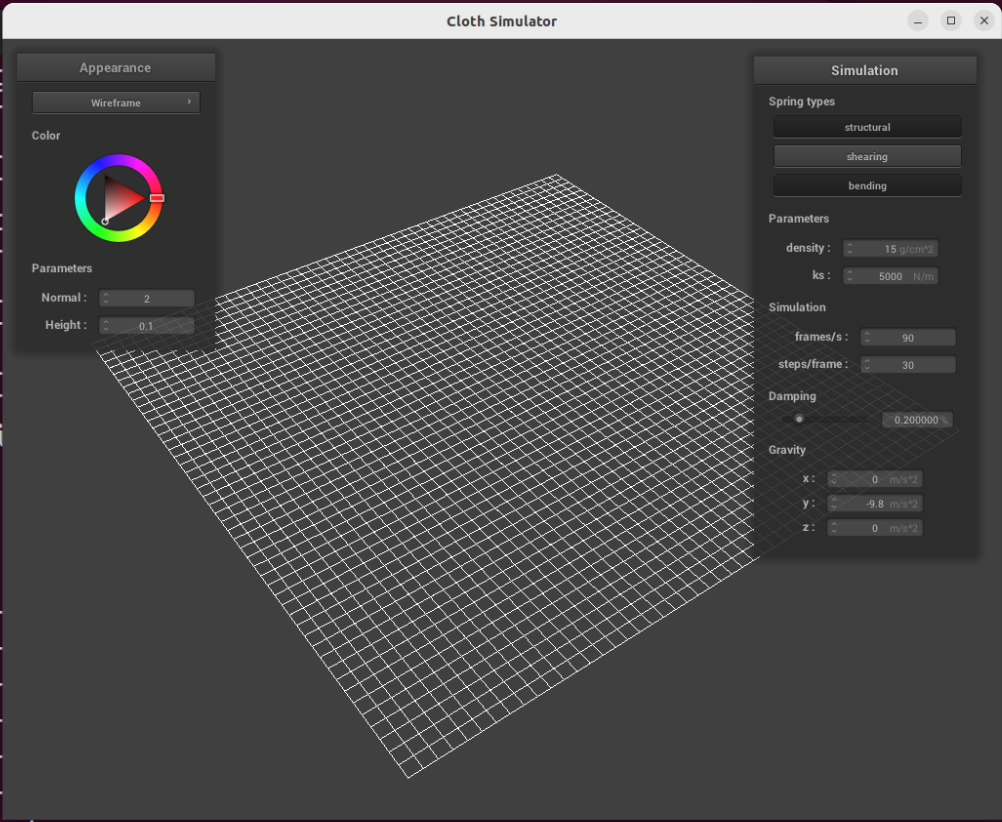
Here’s what the grid looks like:

./clothsim -f ../scene/pinned2.json

Without shearing constraints:

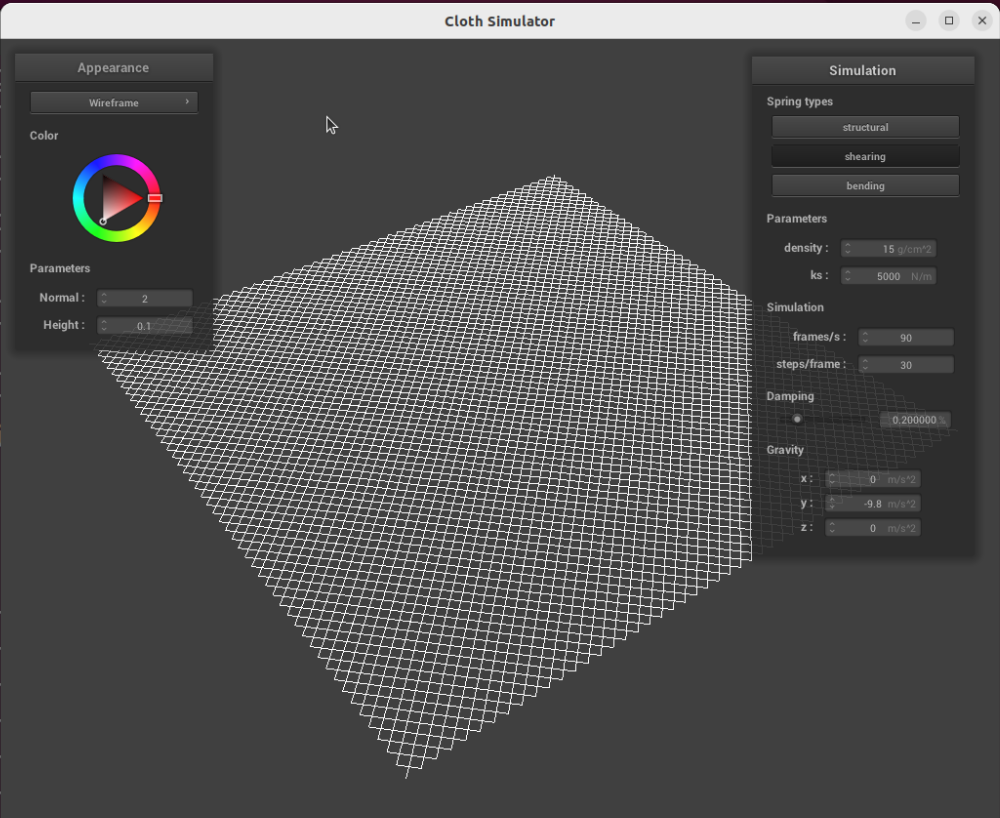
With only shearing constraints:

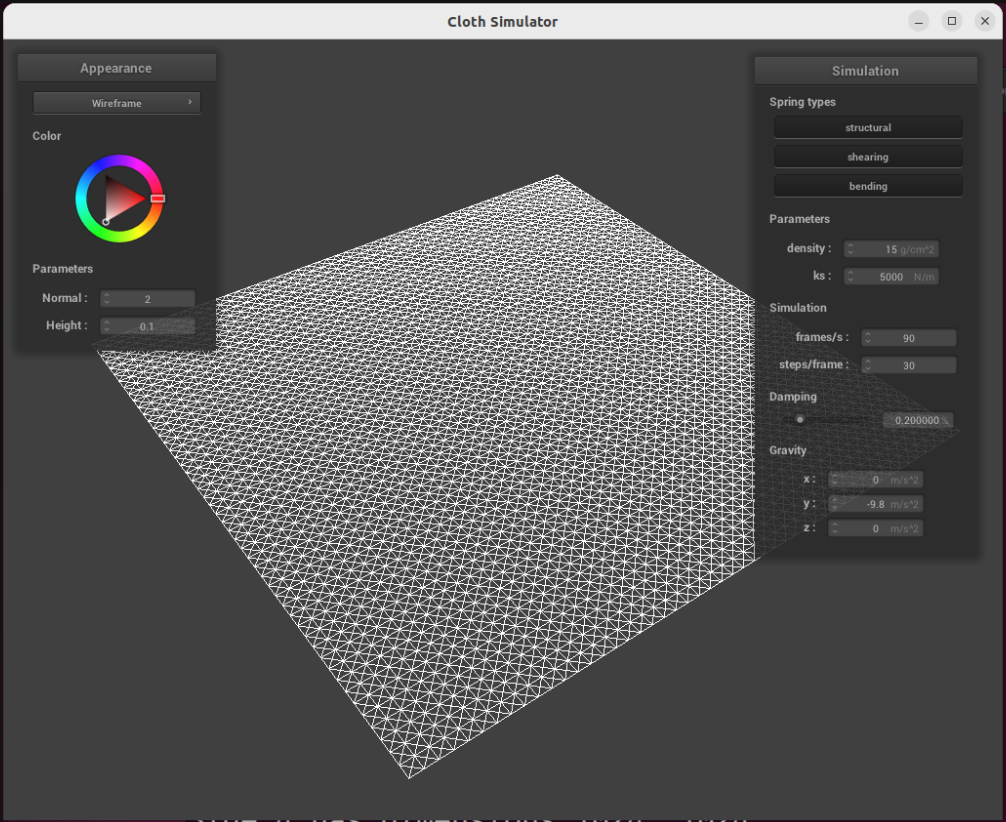
With all constraints:

Part 2: Simulation via Numerical Integration

In this part, we used Verlet integration to update point mass positions based on the total force acting on each point mass (including external forces and spring forces).

For reference, here is the cloth with 4 corners pinned from the scene pinned4.json with default parameters:

Changing the spring constant

The force a spring applies to the two point masses it connects, $a$ and $b$, is calculated using Hooke’s law as follows: $$F_s = k_s \cdot (||p_a - p_b|| - l)$$

where $k_s$ is the spring constant, $p_a$ and $p_b$ are the positions of the two point masses, and $l$ is the rest length of the spring.

When $k_s$ is low, the spring force is low, making the cloth bouncy and fluid. For example, with $k_s = 100 N/m$, the cloth with 4 pinned corners looks like this right after bouncing up for the first time:

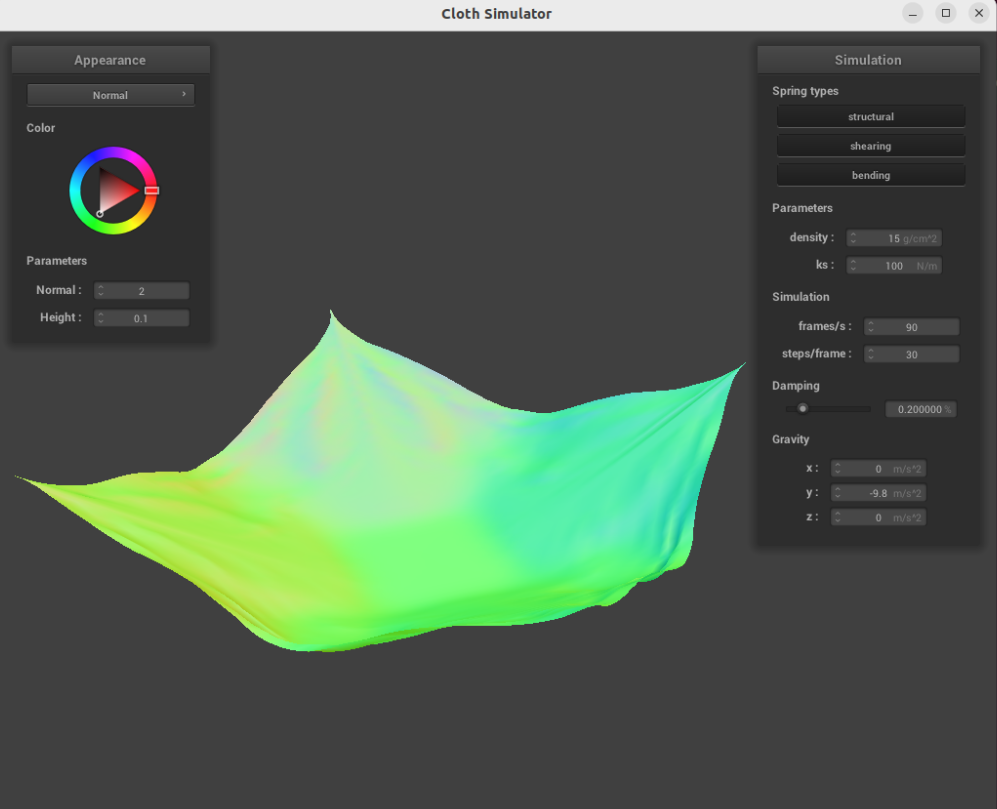
At this low $k_s$ setting, the cloth continues to bounce for a long time before settling into its final rest state.

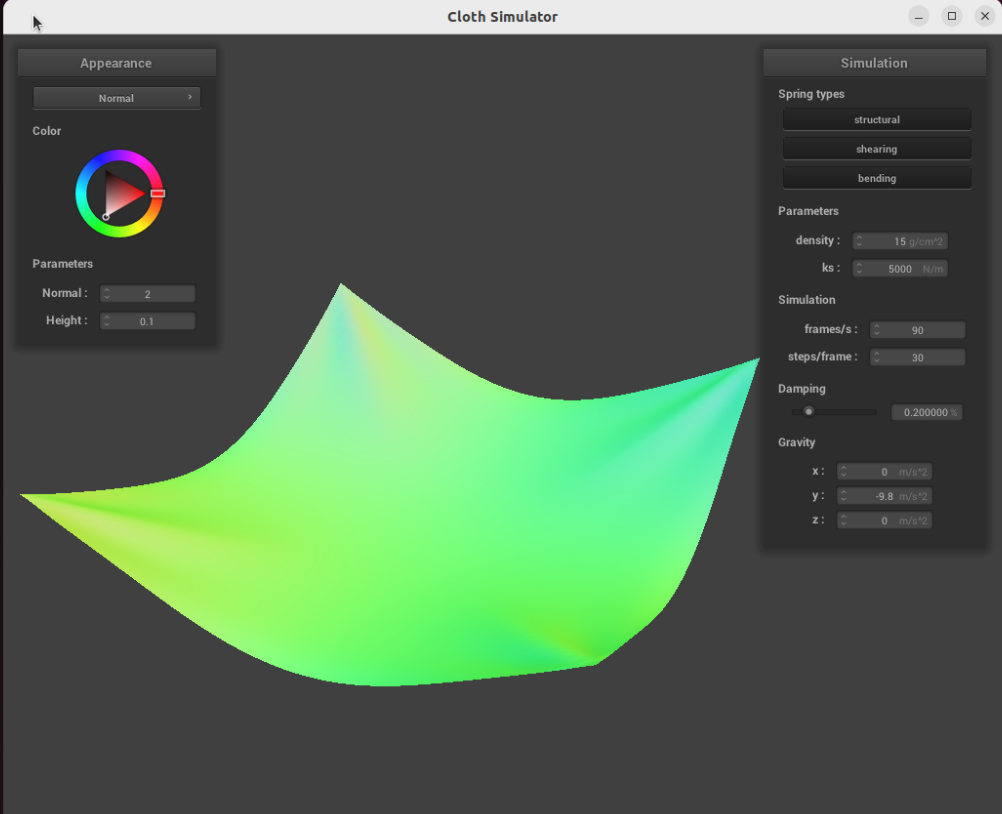
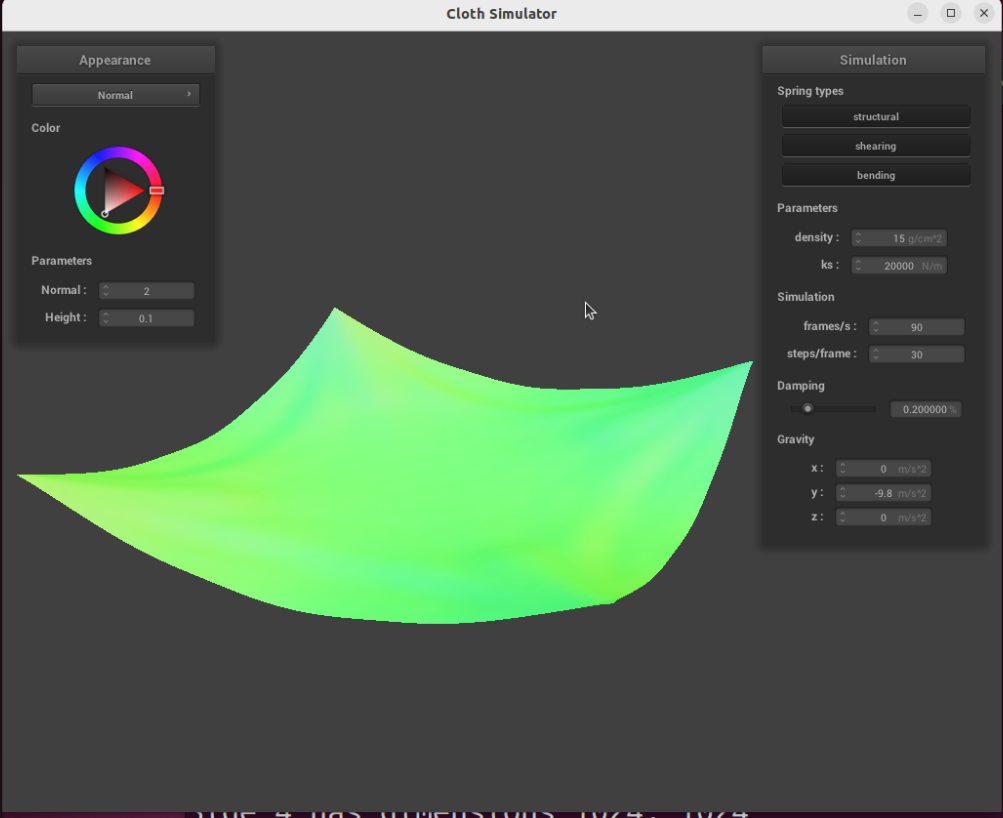
When $k_s$ is high, the high spring forces make the cloth more rigid, so it bounces less and settles more quickly. Here is the same cloth with $k_s = 20000 N/m$ after one bounce:

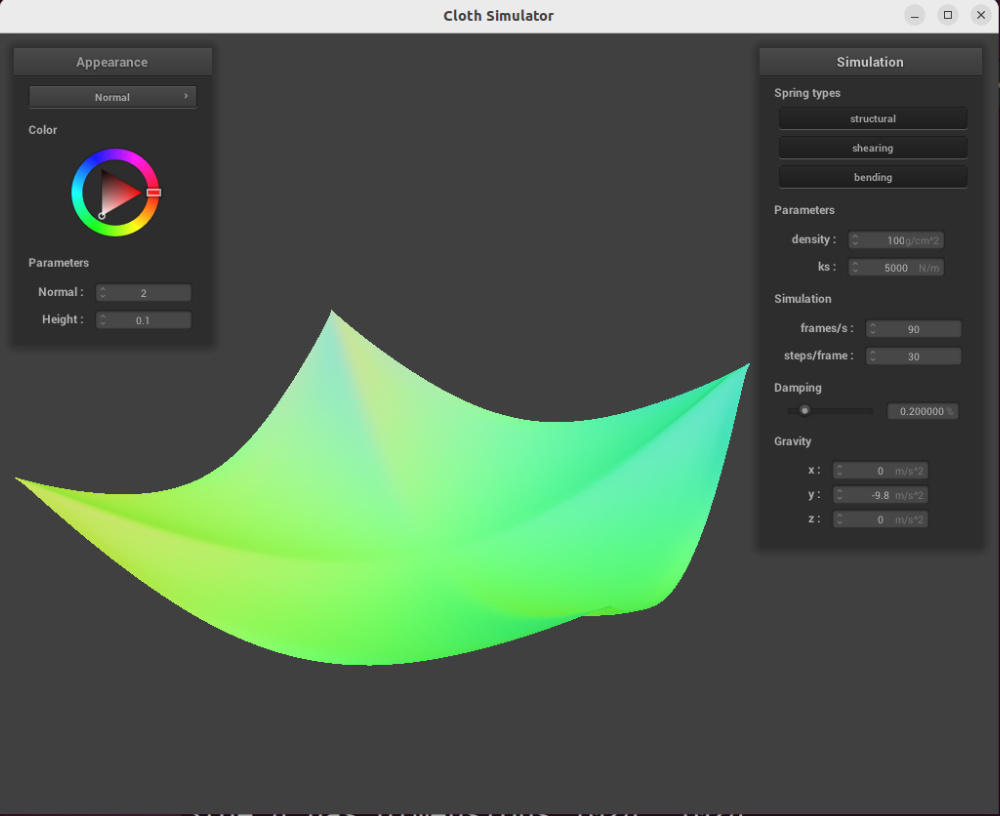
Changing the cloth density

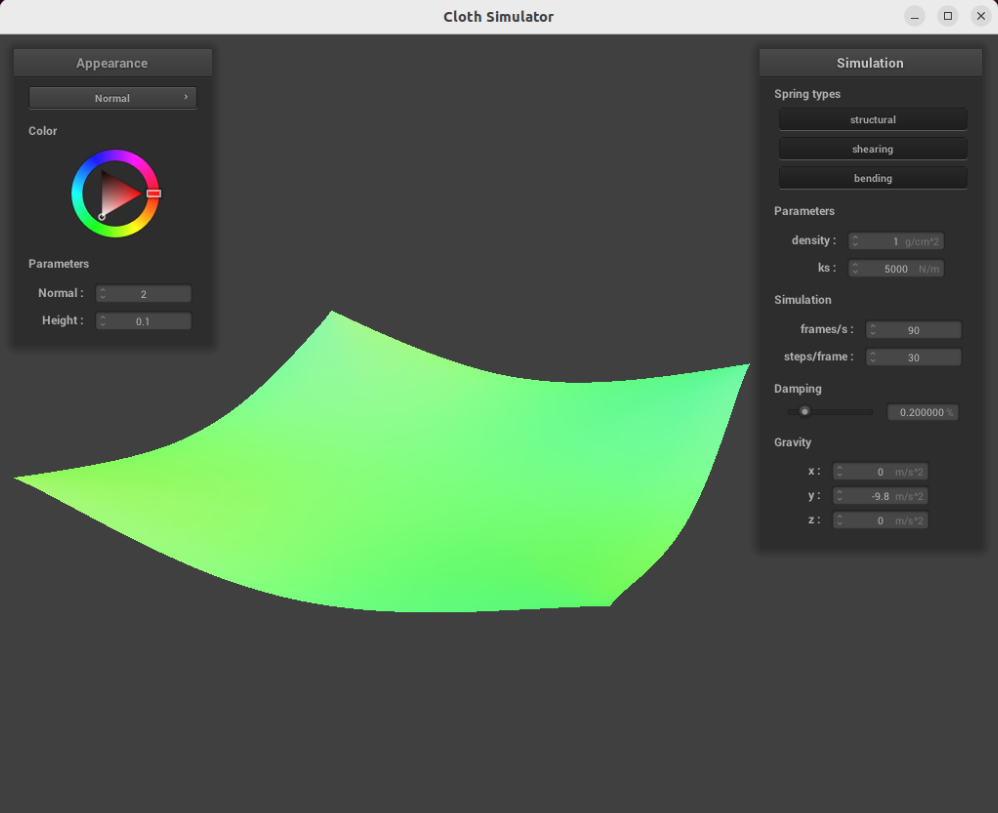
Since $F = ma$, changing the density of the cloth will change its mass (assuming the volume does not change), meaning less force is applied to the cloth.

At a low density ($1 g/cm^2$), the cloth settles into a very shallow bowl shape, and hardly bounces at all while doing so:

On the other hand, at high density ($100 g/cm^2$), the cloth dips much further down and bounces much more when settling into its final position:

Changing the cloth damping

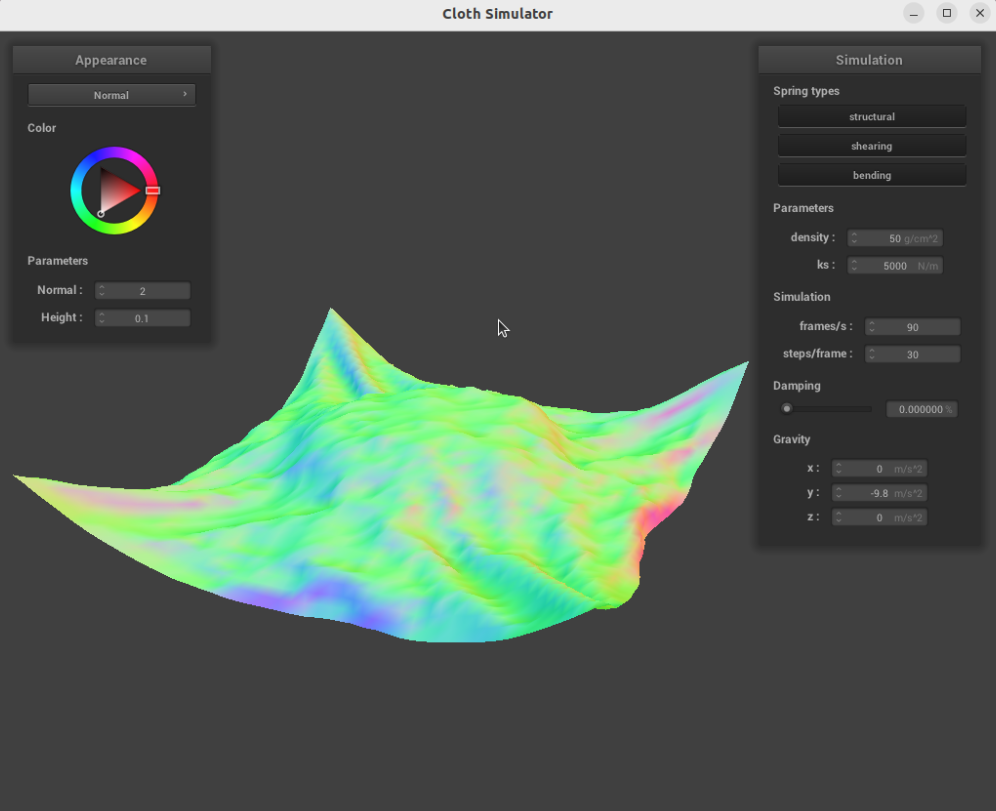
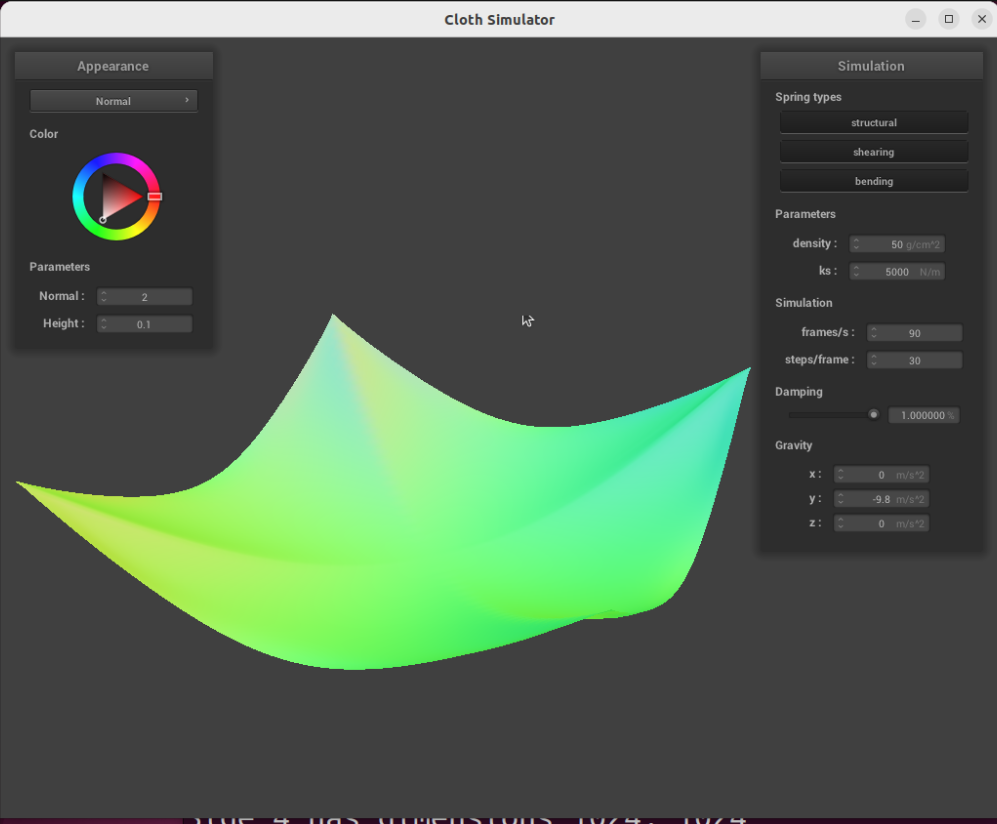
The damping term is analogous to energy loss in the system due to forces such as friction. As the damping term increases, the proportion of velocity allowed into the system each timestep decreases.

With no damping, the cloth moves very quickly, with lots of ripples and bounces:

With maximum damping, the cloth does not bounce at all, and settles immediately into its final rest position:

Part 3: Collisions with Other Objects

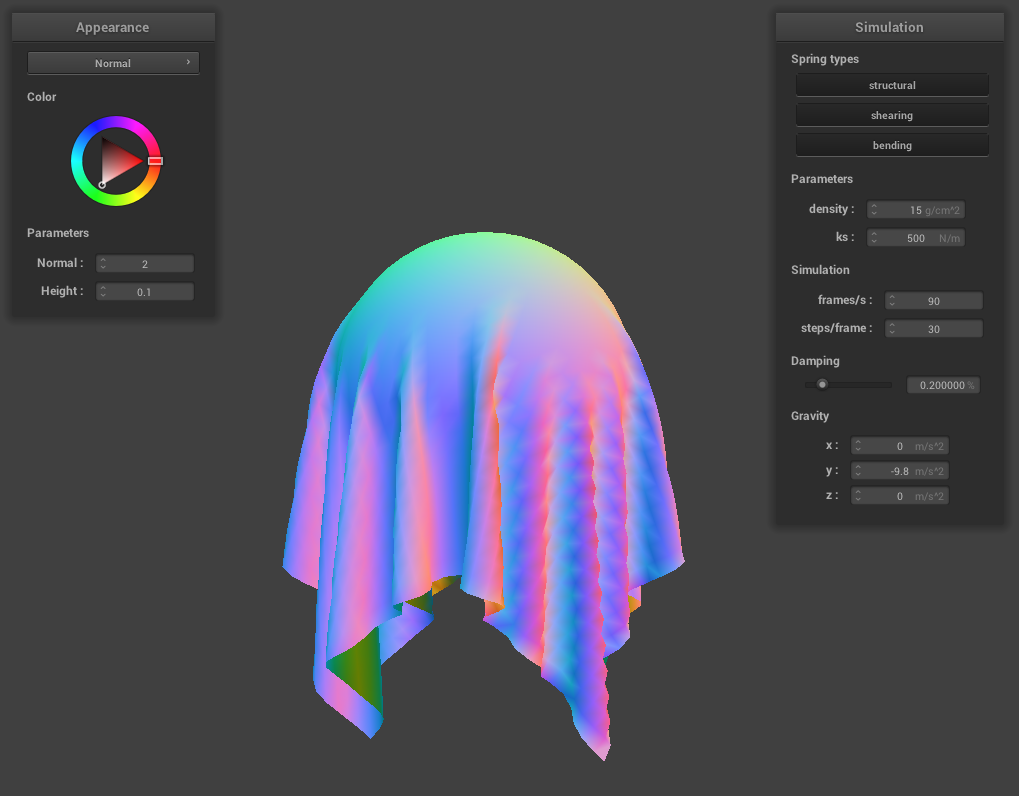
Changing the spring constant

ks = 500

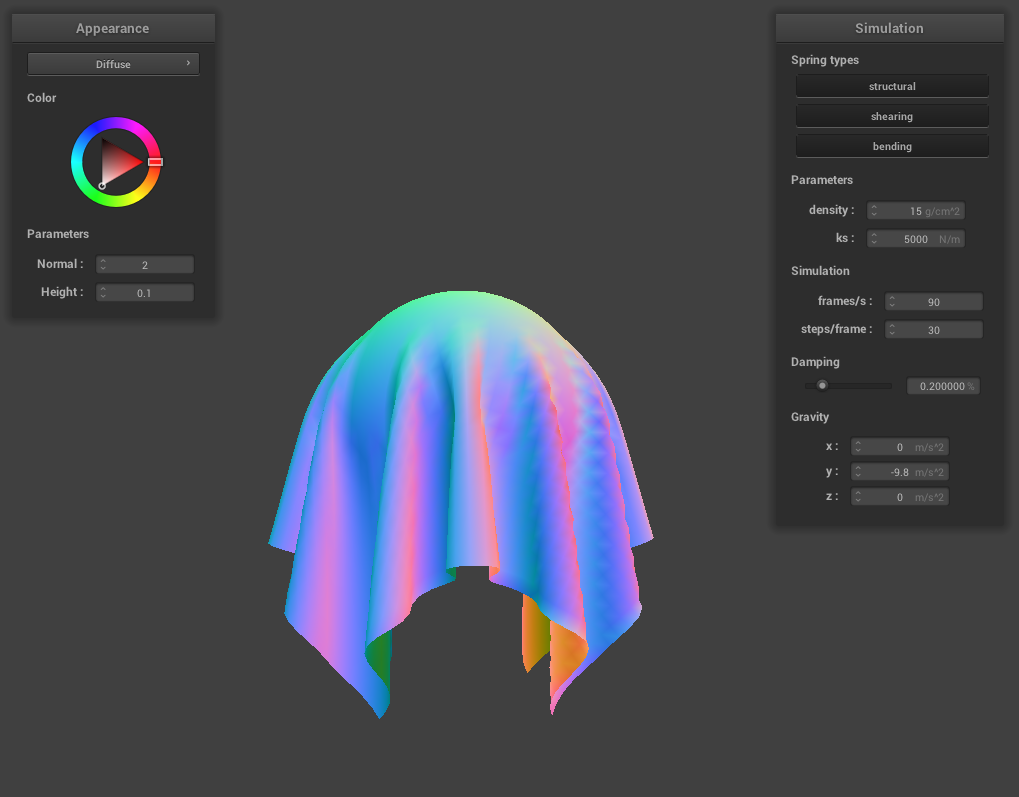
ks = 5000

ks = 50000

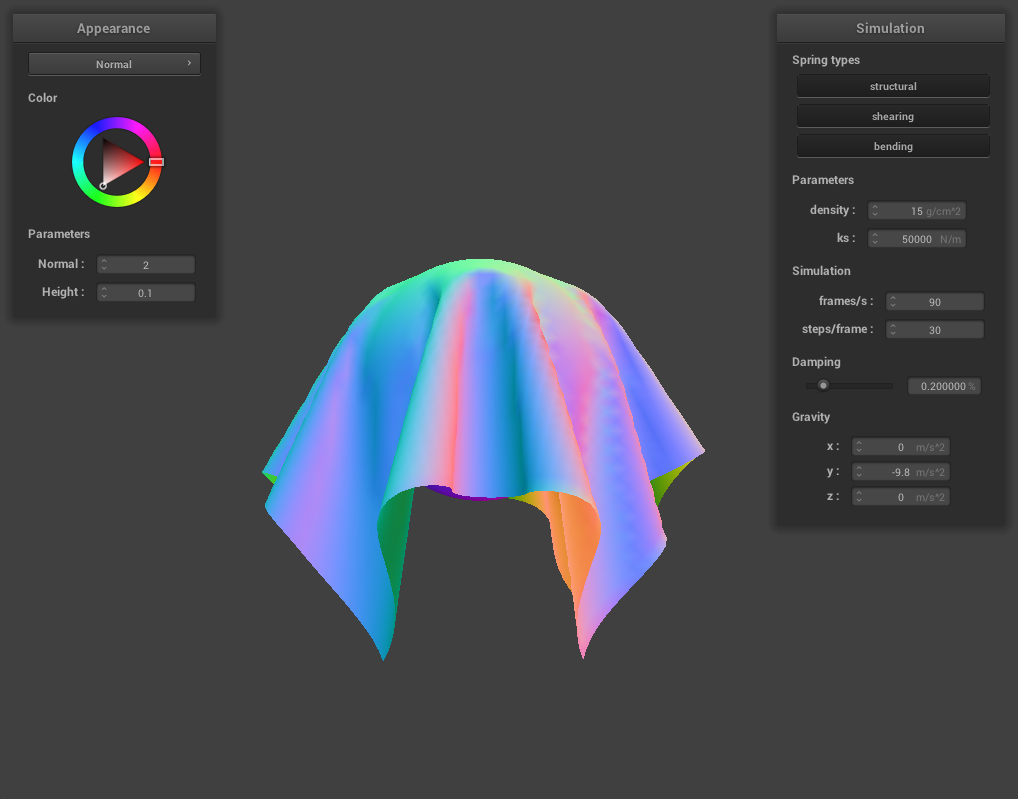
The larger spring constant (ks) causes the cloth to be less tightly draped over the sphere. This is because the higher spring constant provides more force keeping the cloth flat to counterbalance gravity pulling the cloth down around the sphere.

Image of cloth on plane

Part 4: Self-Collisions

Cloth falling steps

Initial collision with the plane

Cloth folding in on itself

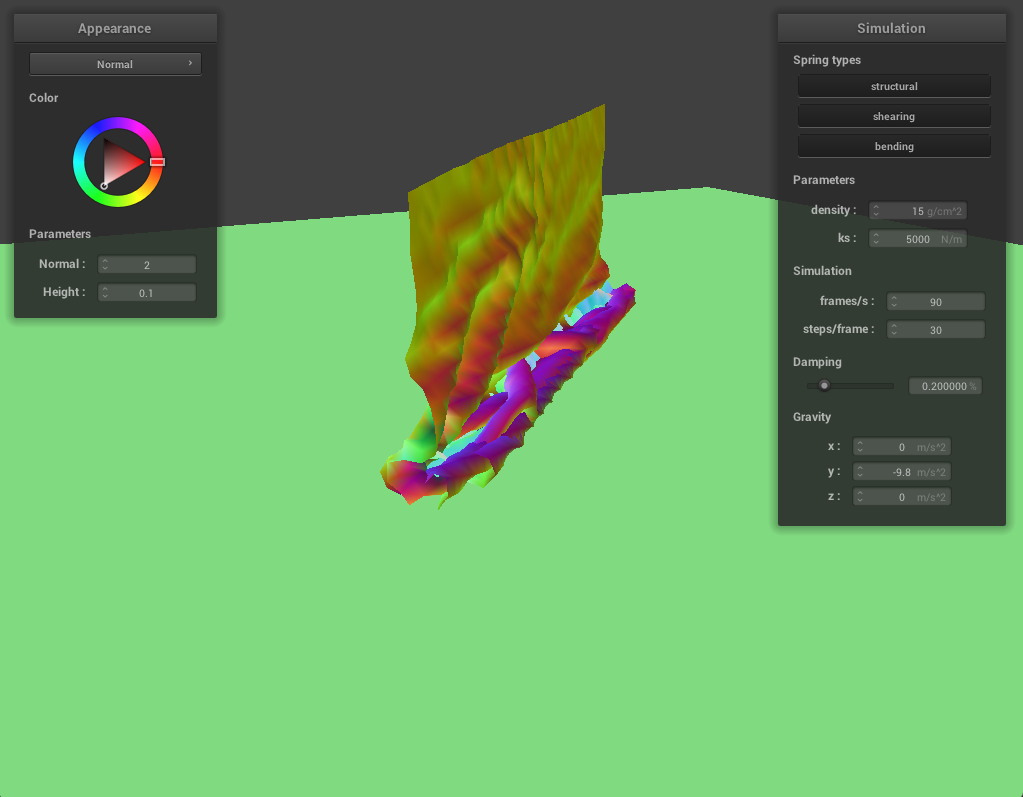
Cloth lying at rest

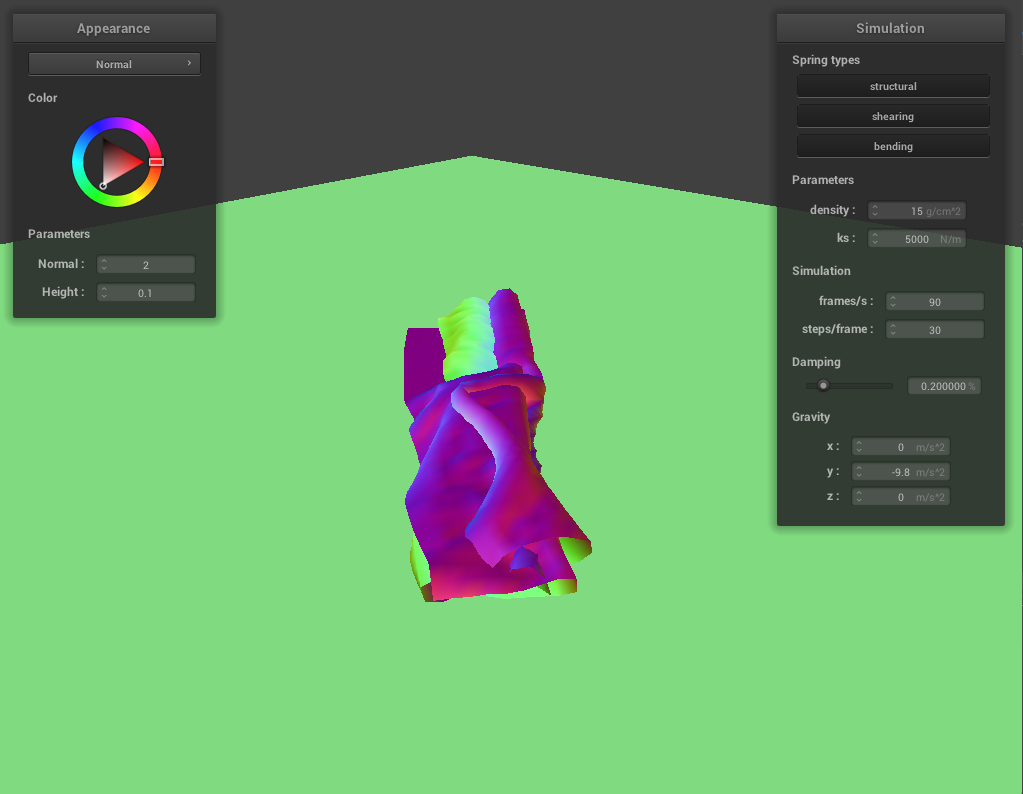
Folded cloth with varying variables

High density

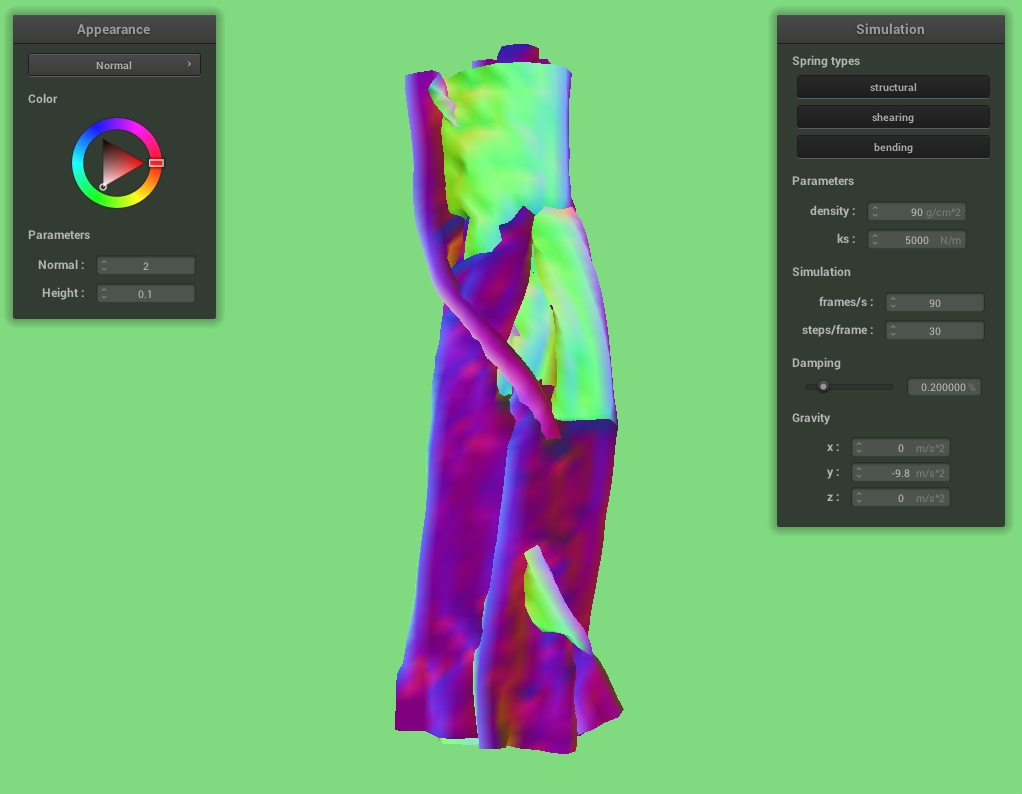
Low density

With a higher density the cloth seems to spread itself out more when it settles.

High spring constant

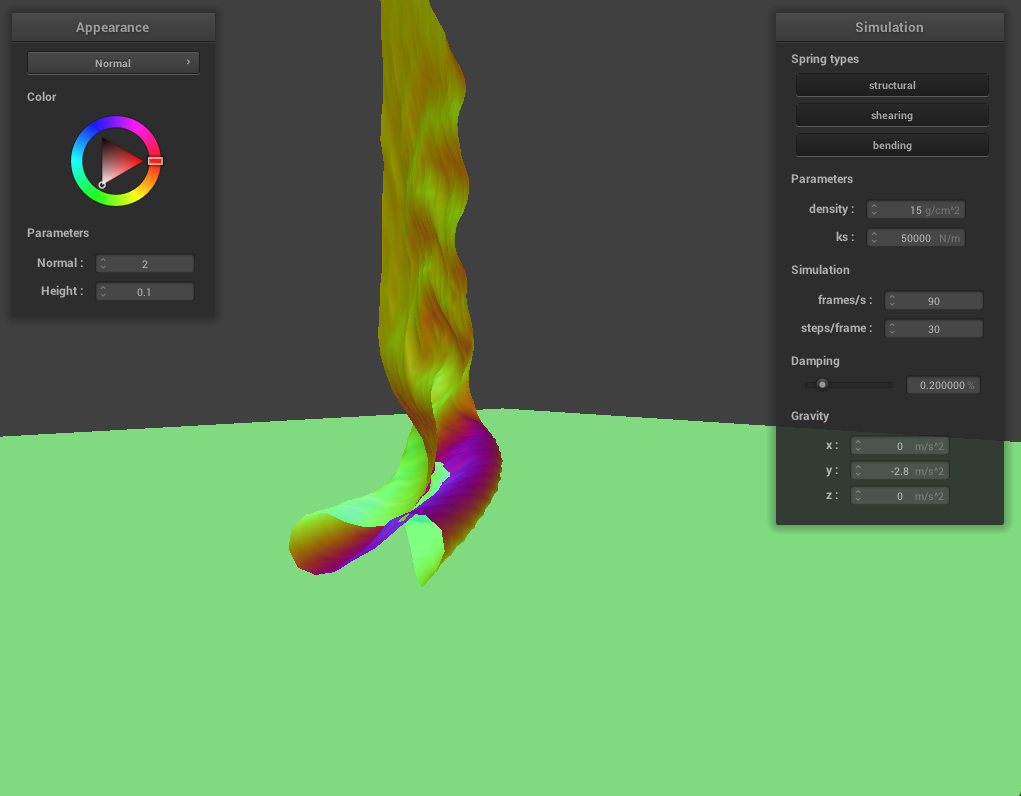
Low spring constant

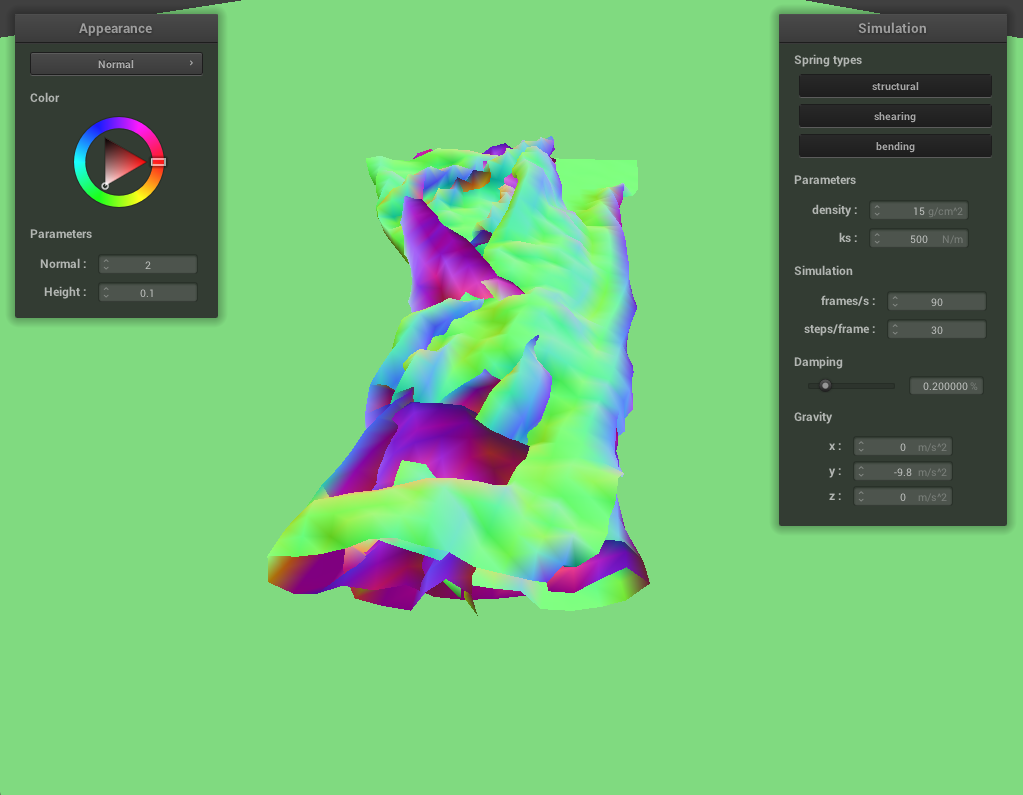
With a high spring constant the cloth does not fold into itself as much, especially while it is initially falling onto the plane. With a low spring constant the cloth folds into itself much more tightly.

Part 5: Shaders

In this section, we implemented a variety of shaders for the cloth.

A shader program computes the color at every point on objects in the scene based on parameters such as the position, normal direction, lighting, color, and texture map. The vertex and fragment shaders work together: vertex shaders help create material effects by varying the appearance and position at vertices in the object, while fragment shaders fill in the spaces between vertices during rasterization.

Blinn-Phong

The Blinn-Phong shading model is a method of rendering lighting effects based on material properties. It does this by combining three different types of lighting:

• Ambient lighting does not depend on the position on the object; it is constant throughout the scene.
• Diffuse lighting creates the matte appearance of an object by varying intensity based on how far away a point is from the light.
• Specular lighting creates the shiny reflections of an object by creating a very concentrated version of diffuse lighting through exponentiation of the lighting component, such that large values become extremely bright and small values become negligible.

Here is the Blinn-Phong model with only ambient lighting:

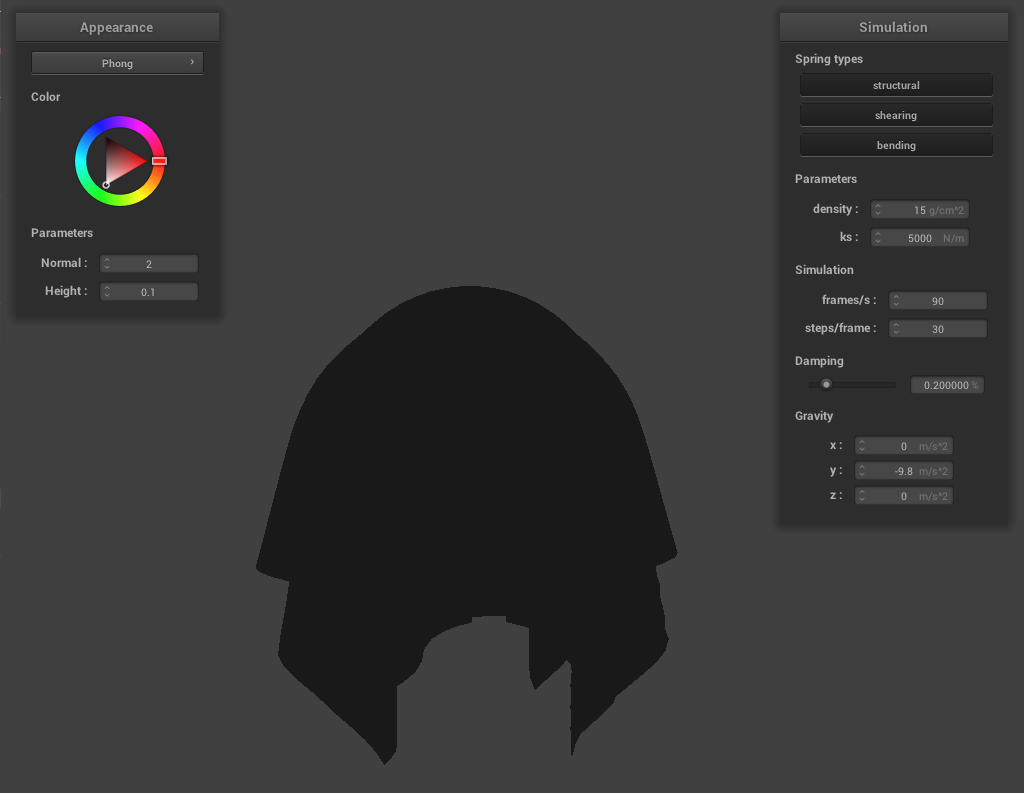
With only diffuse lighting:

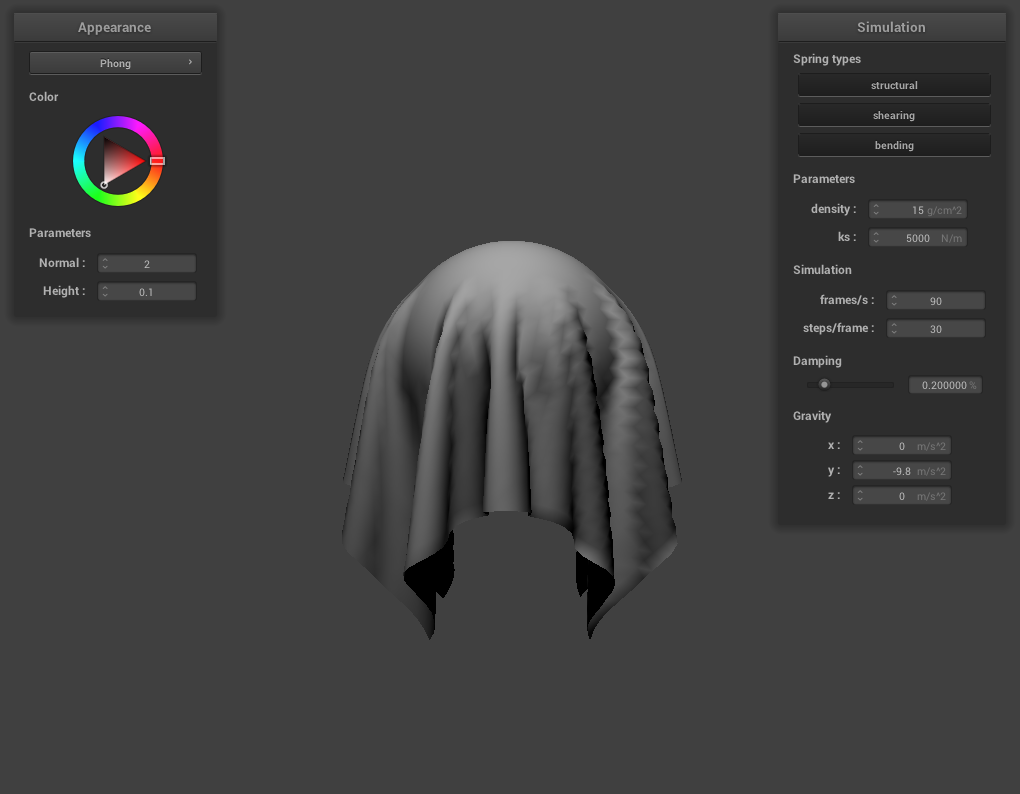
With only specular lighting:

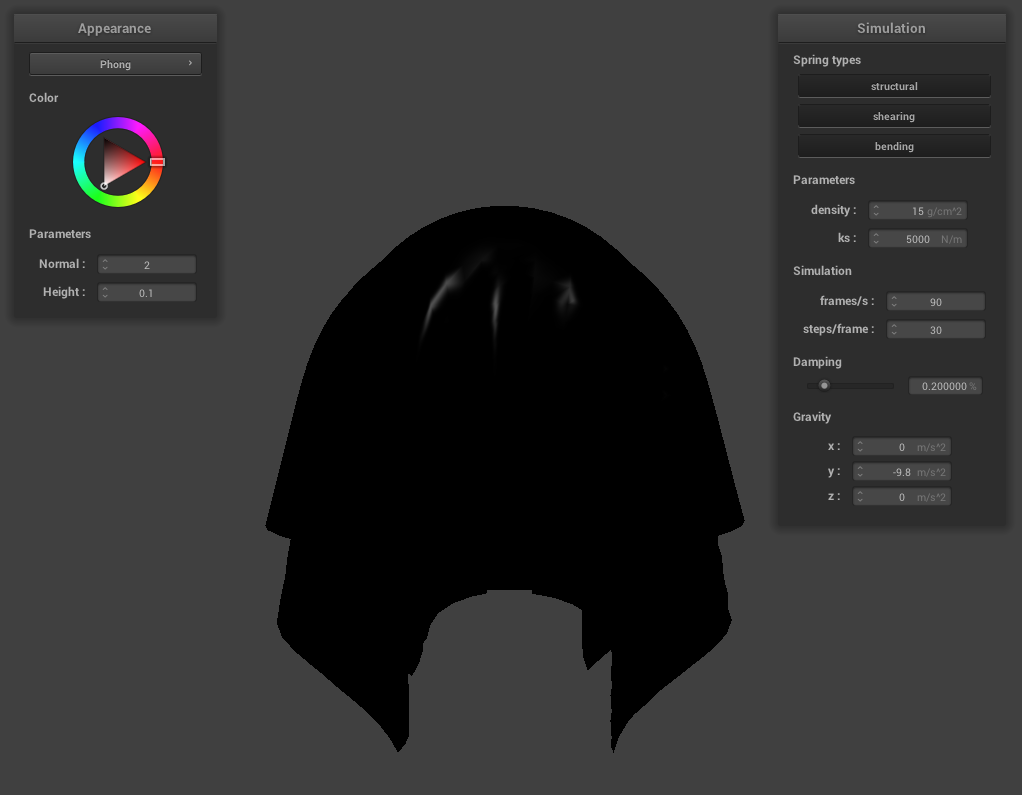
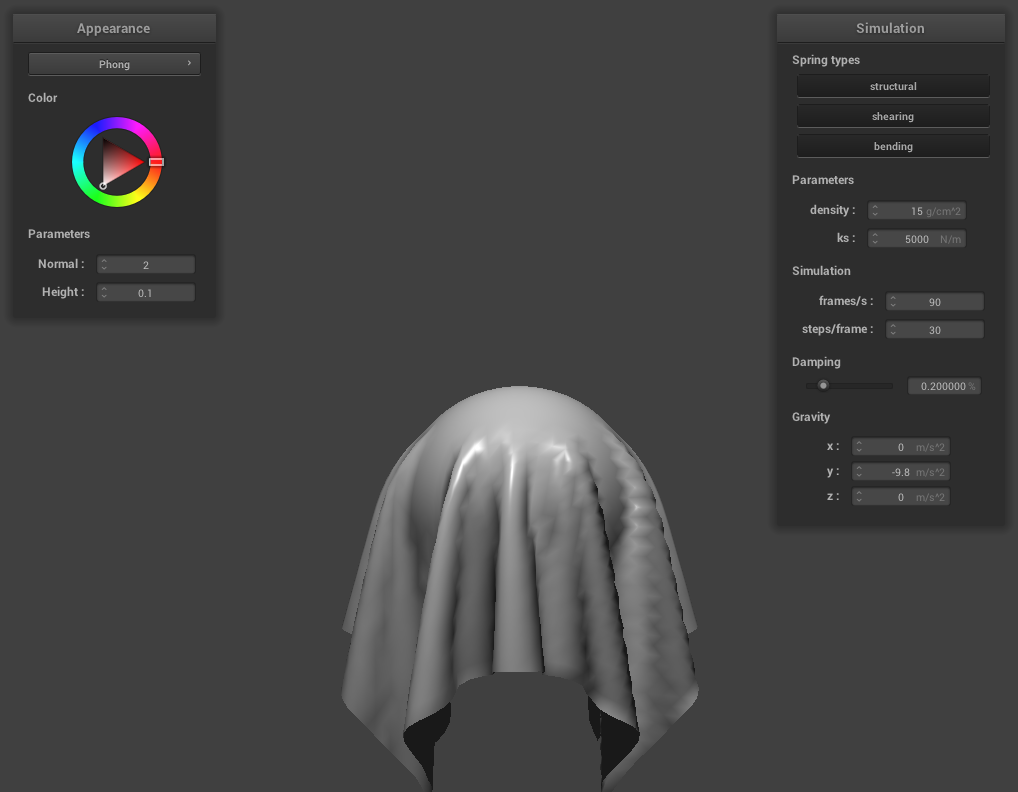
With all lighting:

Texture Mapping

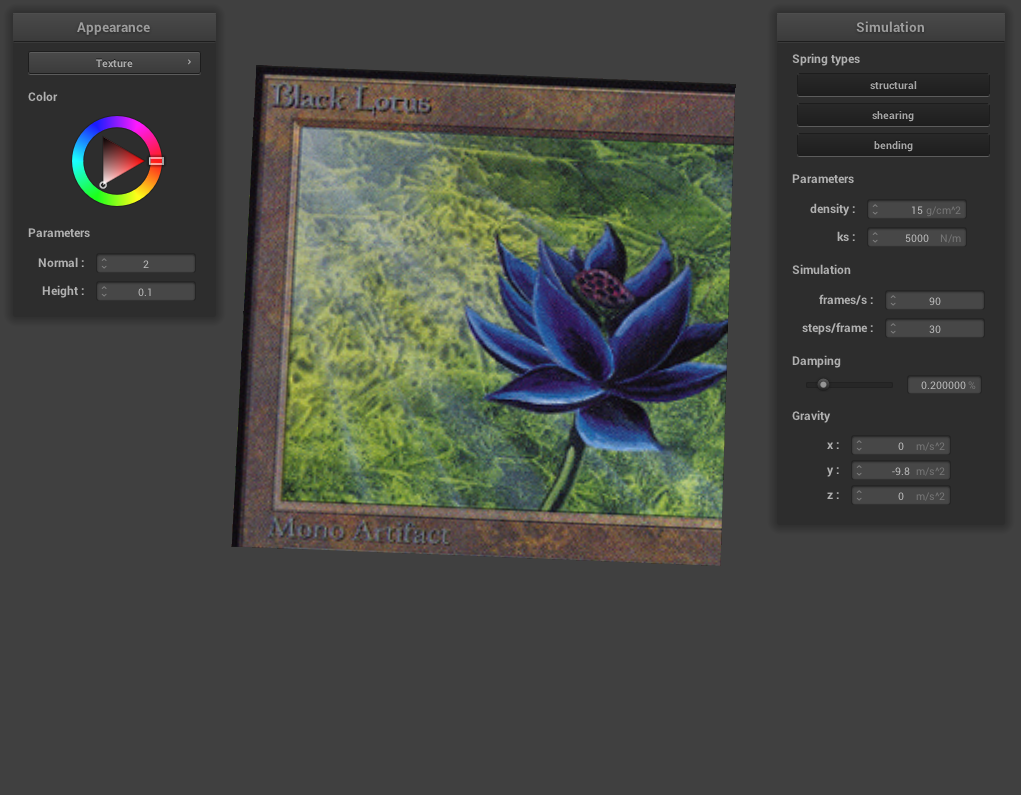
Here’s our custom texture, the Black Lotus card:

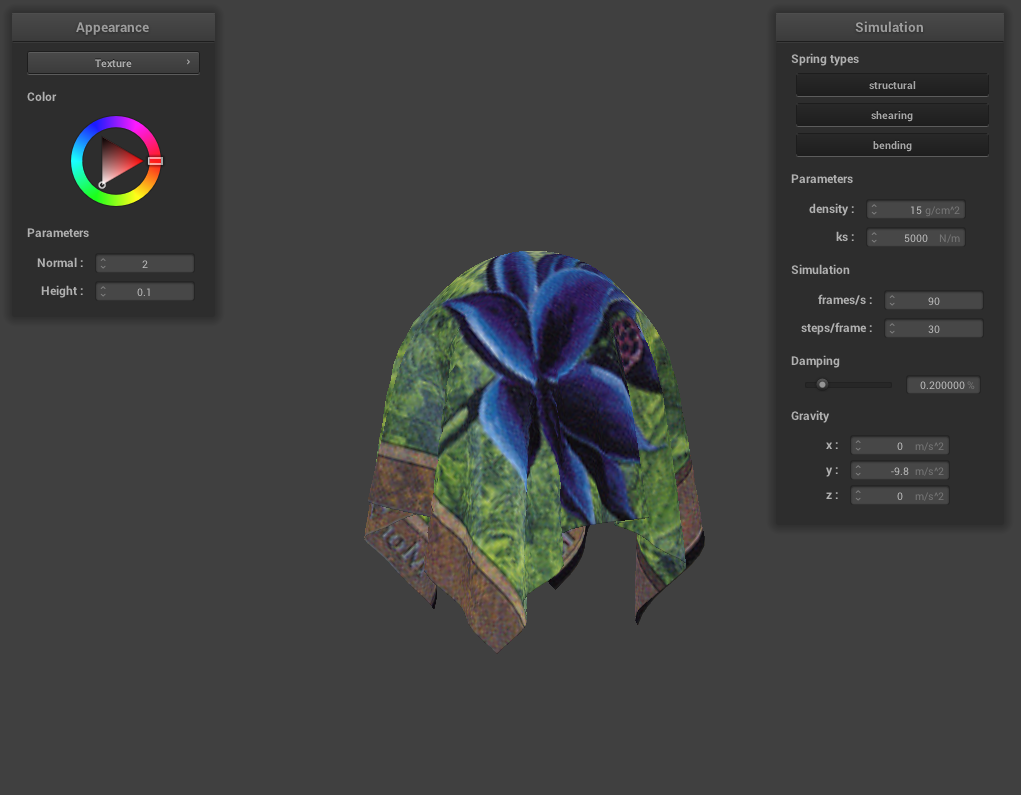
This is what the cloth looks like with this texture:

This is the same cloth as above, after falling on the sphere:

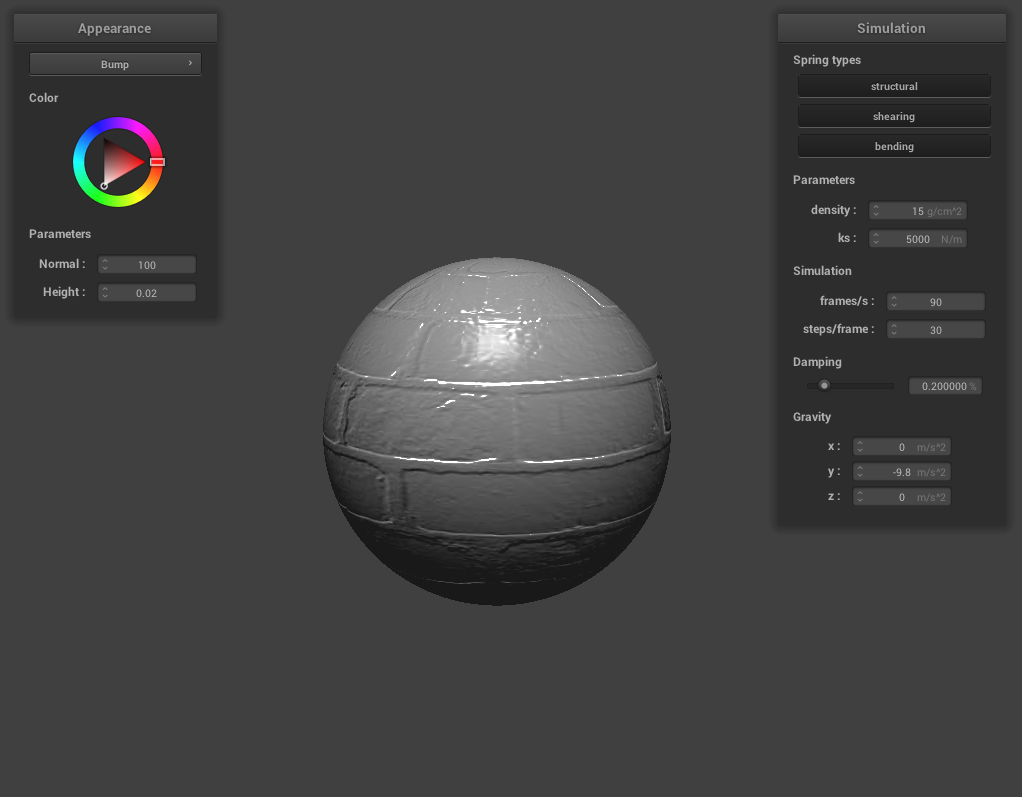
Bump and Displacement Mapping

Here’s the bump-mapped sphere using the brick texture_3.png:

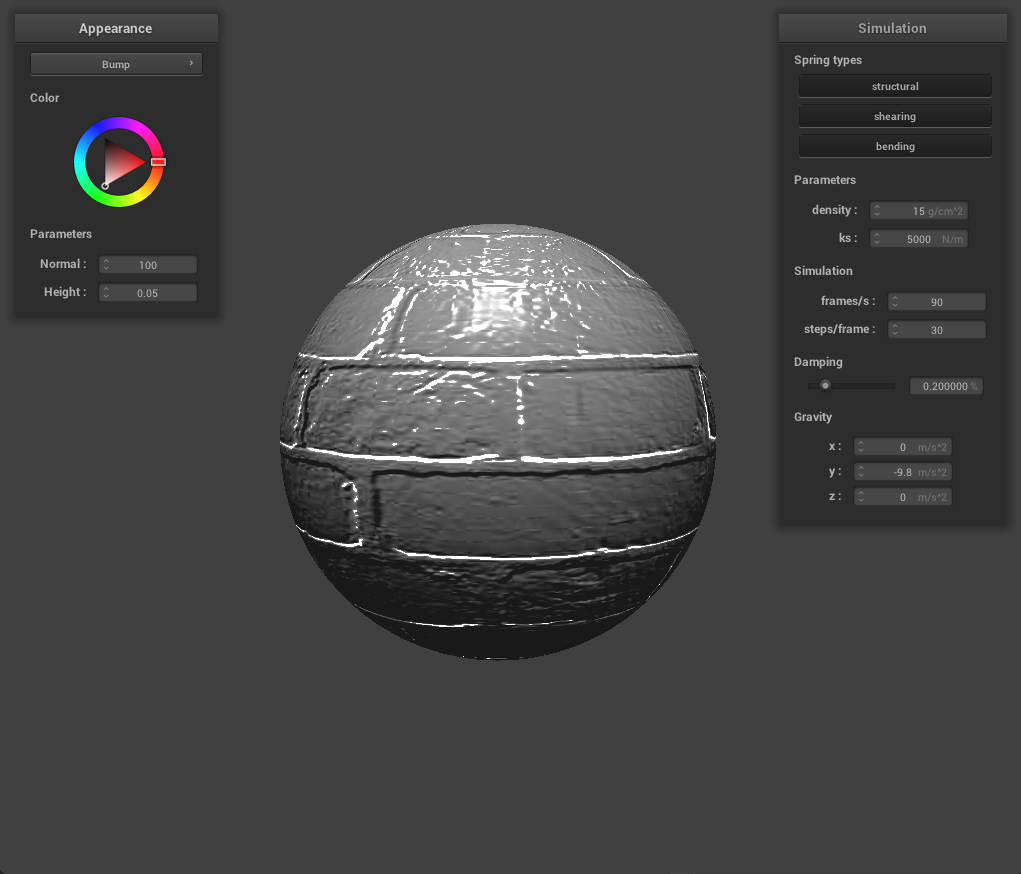
Here’s the displacement-mapped sphere using the same texture:

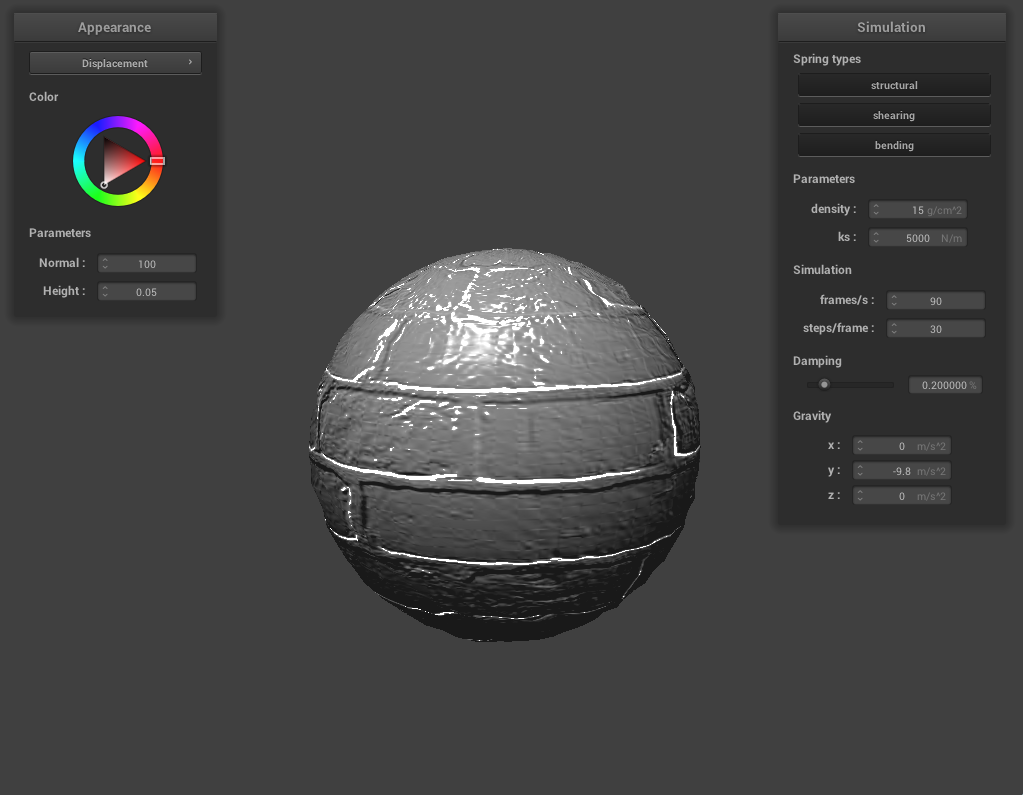
Now, here’s the same images with coarseness values -o 16 -a 16:

(Bump)

(Displacement)

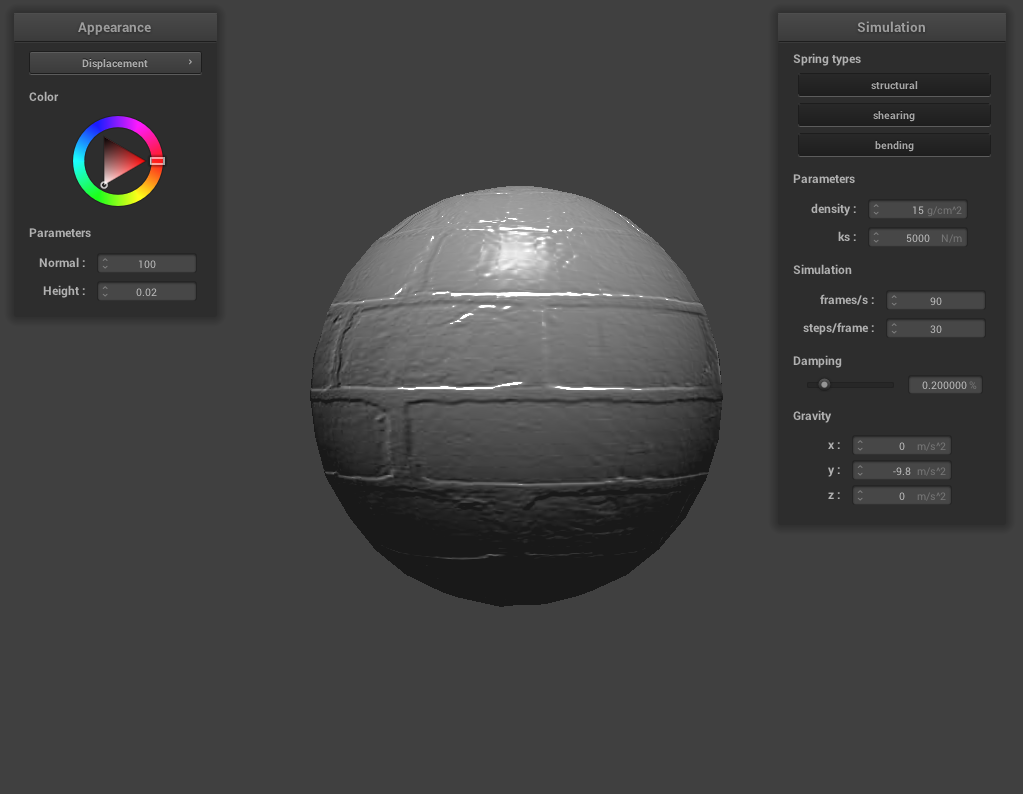
And for -o 128 -a 128: (Bump)

(Displacement)

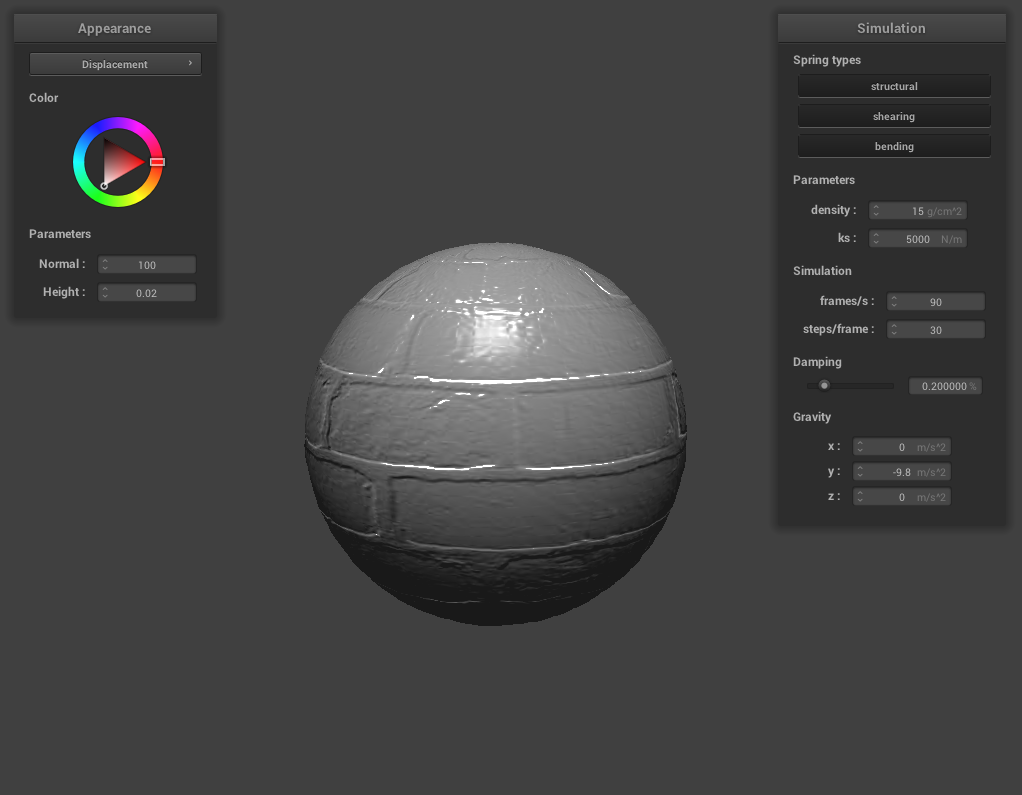
As we can see from the above images, there doesn’t seem to be a very large difference in the coarseness.

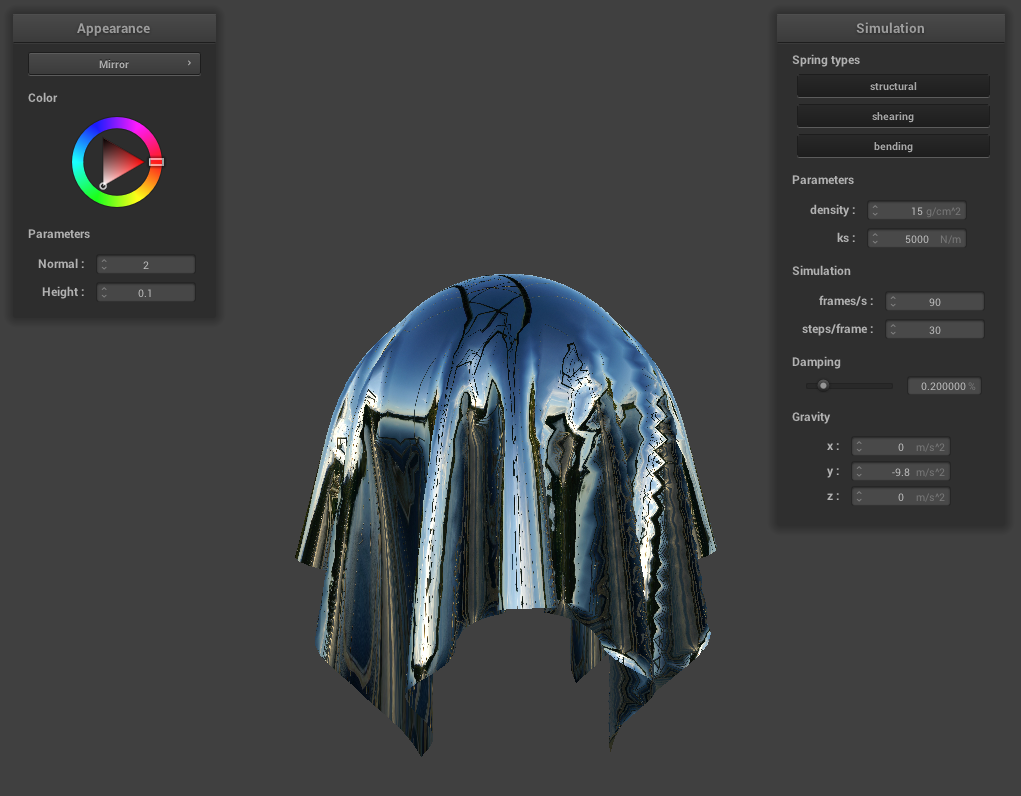
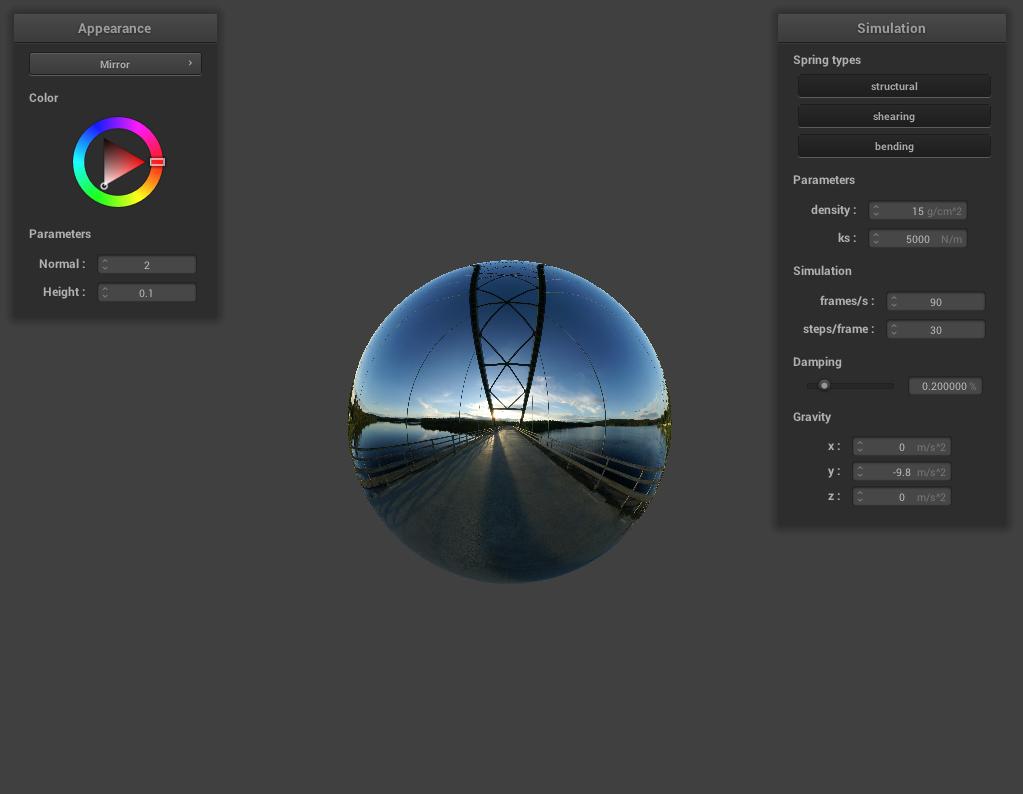
Mirror Shading

Here’s a screenshot of the mirror shading on the cloth and sphere:

Mirror Sphere

Mirror Cloth